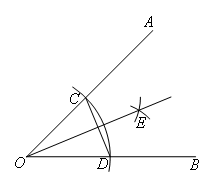
如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D.再分别以点C,D为圆心,大于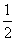CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是(    )

解：选项A：
连接CE，DE，根据作图得到OC=OD，CE=DE．
∵在△EOC与△EOD中，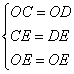

∴△EOC≌△EOD（SSS），
∴∠AOE=∠BOE，即射线OE是∠AOB的平分线，正确，不符合题意；
选项B：
根据作图得到OC=OD，
∴△COD是等腰三角形，正确，不符合题意；
选项C：
根据作图得到OC=OD，
又∵射线OE平分∠AOB，
∴OE是CD的垂直平分线，
∴C，D两点关于OE所在直线对称，正确，不符合题意；
选项D：
根据作图不能得出CD平分OE，
∴CD不是OE的平分线，
∴O，E两点关于CD所在直线不对称，选项D错误，符合题意．
故选D．

略