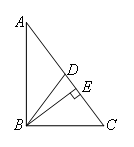
如图,BD,BE是直角三角形ABC斜边AC上的中线与高线.已知AB=4,BC=3,则AD:DE:EC等于(    )

1．思路分析：
①梳理信息，明确目标．本题要求三条线段长度之比，明显需要计算出各线段长．
②合理转化与计算．BD是斜边中线，直接计算得斜边长一半；BE为斜边上的高，根据等积公式可计算得BE，再根据勾股定理可得DE长，DC-DE即为EC；
2．解题过程：

故选C．
3．易错点
未掌握等积公式，不能计算出高BE的长；
不能在△BDE中灵活使用勾股定理，进而计算DE长．
4．推荐视频
如果此题有问题，推荐查看视频：“2013~2014八年级上册数学拔高训练北师版，第一讲直角三角形性质应用，直角三角形斜边中线”
http://v.xxt.cn/course/courseview.do?courseId=1598&videoId=11720

略