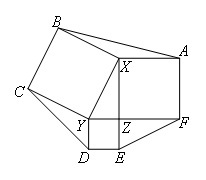
如图，分别以Rt△XYZ的直角边和斜边为边向外作正方形AXZF，
正方形BCYX，正方形DEZY，若直角边YZ=1，XZ=2，则六边形ABCDEF的面积为____.

1.思路分析
本题主要考查弦图模型的识别以及特殊图形面积的计算．处理此类问题需要：
①明确目标，确定思路．本题要求的是六边形的面积，适合借助图形分割求和计算．
②梳理条件，构造模型．题干条件中明确△XYZ是直角三角形，且直角边边长已知，可知三个正方形的面积及△XYZ、△ZEF的面积容易求解，△DCY、△ABX需要做高求解．因此分别过B作AX的高线，过C作DY的高线，可构造出赵爽弦图模型．
③转化计算，结果验证．根据弦图模型可分别计算△DCY、△ABX的面积，最后对分割的小块图形进行面积求和，得出结果．
2.解题过程
如图，过B作AX的垂线，交AX延长线于点M；过C作DY的垂线，交DY延长线于点N；（补成赵爽弦图）

在Rt△XYZ中，YZ=1，XZ=2
∴由勾股定理可知，
∴；
∵△XYZ≌△FEZ
∴；
∴；；；
由弦图可知，△BMX≌△XQY；△YNC≌△XQY
∴BM=XQ；CN=QY
∵四边形QYZX是长方形
∴XQ=YZ=1，QY=XZ=2
∴BM=1，CN=2
∴；

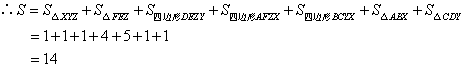
3.易错点
不能识别出弦图模型．
4．推荐视频
如果此题有问题，建议观看视频：“2013~2014八年级上册数学拔高训练北师版，初中数学勾股定理拔高课，第1讲直角三角形性质应用，05弦图结构”
视频连接：http://v.xxt.cn/course/courseview.do?courseId=1598

略