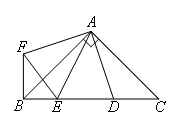
如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①△AEF≌△AED;②∠AED=45°;③BE+DC=DE;
④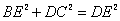,其中正确的是(    )

1．思路分析
本题主要考查旋转的性质及勾股定理的使用，解决此类问题需要清楚：
①旋转是全等变换，旋转前后对应边、对应角相等；
②几何问题处理注意读题标注，多条件进行整合．
2．解题过程
在Rt△ABC中，AB=AC
∴∠ABC=∠ACB=45°
由旋转可知，△ACD≌△ABF
∴CD=BF，AD=AF，∠ACB=∠ABF，∠CAD=∠BAF
∴∠EBF=90°，∠FAD=90°
∵∠DAE=45°
∴∠FAE=∠DAE
在△DAE和△FAE中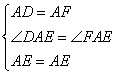

∴△DAE≌△FAE，①正确；
∵△BEF是直角三角形
∴，④正确．
∵∠DAE=45°
若∠AED=45°，则∠ADE=90°，与题干不符，故②错误；
在Rt△BEF中，
BE+BF>EF，即BE+CD>DE，故③错误．
故选B．
3．易错点
没有对旋转导致全等的条件进行合理转化，转移边、角不到位，导致没有思路解题．

略