如图,在等腰Rt△ABC中,∠A=90°,AC=9,点O在AC上,且AO=2,点P是AB上一动点,连接OP将线段OP绕O逆时针旋转90°得到线段OD,要使点D恰好落在BC上,则AP的长等于( )
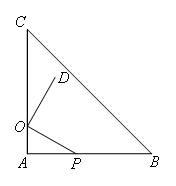
- A.2
- B.
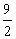
- C.5
- D.7
答案
正确答案:C
1.思路分析
本题主要考查旋转的性质,以及借助特殊的角度表达线段长求解等.解决此类问题需要注意:
①读题标注,根据题意画图.本题需画出示意图,便于理解题意.
②梳理条件,挖掘特征,合理转化.本题中根据旋转的特征,可借助线段相等找全等三角形,表达线段长.
③借助旋转、全等性质建等式求解.通过全等的性质,借助特殊角度表达线段长求解.
2.解题过程
如图,过点D作DE⊥AC于E,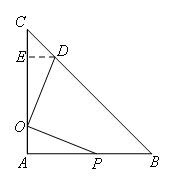
则∠DOE+∠AOP=90°,∠DOE+∠ODE=90°
∴∠ODE=∠AOP
又∵OD=OP,∠DEO=∠OAP=90°
∴△DEO≌△OAP,
∴DE=OA=2
∵∠C=45°,∠DEC=90°
∴CE=DE=2
∴AP=OE=9-2-2=5
故选C
3.易错点
不能根据题意画出示意图,理解题意有偏差.
没能利用好旋转的结构和等腰直角三角形的特殊条件进行线段长的转移.
略








