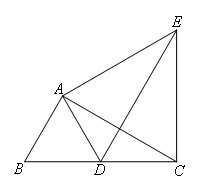
如图,将含30°角的直角三角板ABC绕直角顶点A逆时针旋转到△ADE的位置,使B点的对应点D落在BC边上,连接EC,则下列结论:①∠DAC=∠DCA;②ED所在直线为AC的垂直平分线;③△ACE是等边三角形;④ED=2AB.其中正确的是(    )

结论①根据旋转的性质可得：AB=AD，因为∠ABD＝60°，
所以△ABD是等边三角形，
由此可以知道∠DAC＝30°，所以∠DAC＝∠DCA，①正确；
结论③根据旋转性质可得：AC＝AE，∠EAC＝60°，
所以△ACE是等边三角形，③正确；
结论②根据①③可得：AD＝DC，AE＝CE，即D，E到线段AC两端的距离相等，
则D,E在AC的垂直平分线上，②正确；
结论④根据旋转的性质可得：DE＝BC，因为BC＝2AB，
所以ED＝2AB，④正确．
综上：①②③④都正确．
故选D

略