如图,在Rt△ABC中,
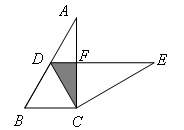
ACB=90°,A=30°,BC=2,将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为( )
ACB=90°,
- A.30,2
- B.60,2
- C.60,
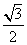
- D.60,
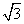
答案
正确答案：C
知识点：等边三角形的判定与性质 旋转的性质 三角形的面积 含30度角的直角三角形
根据旋转的性质可得，DC=BC=2，
∵∠ACB=90°，∠A=30°，
∴∠B=90°-30°=60°，
∴△BCD是等边三角形，
∴∠BCD=60°，
∴n=60．
∵∠DCA=90°-∠BCD=30°，∠EDC=∠B=60°，
∴∠CFD=180°-30°-60°=90°，
在Rt△CDF中，∠DCF=30°，DC=2，
∴
，
，阴影部分的面积为
．
略
WORD格式（
