如图,在Rt△ABC中,AB=AC,∠BAC=90°,D,E为BC边上两点,∠DAE=45°,将AE绕点A顺时针旋转90°得到AF,连接BF,EF.则下列结论:①CE=BF;②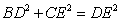 ;③
;③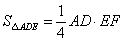 ;
;
④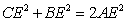 .其中正确的是( )
.其中正确的是( )

- A.①②③④
- B.①②④
- C.①③④
- D.②③
答案
正确答案:A
①由旋转的定义及性质知,∠EAF=90°,AE=AF,
∵∠BAC=90°,
∴∠CAE=∠BAF,
在△ACE和△ABF中,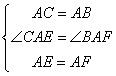
∴△ACE≌△ABF(SAS),
∴CE=BF,故①正确.
②如图,连接DF,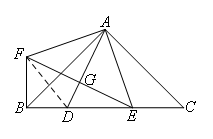
由①知,△ACE≌△ABF,
∴∠C=∠ABF=45°,
∴∠DBF=90°.
∵∠EAF=90°,∠DAE=45°,
∴∠DAF=45°,
∴∠DAE=∠DAF,
在△EAD和△FAD中,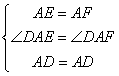
∴△EAD≌△FAD(SAS),
∴DE=DF,
在Rt△BDF中,由勾股定理,得![]()
∴![]() 故②正确.
故②正确.
③在等腰Rt△AEF中,∠DAE=∠DAF,
∴AG⊥EF,EF=2EG,
∴![]() ,
,
故③正确.
④在等腰Rt△AEF中,由勾股定理,得![]() ,
,
在Rt△BEF中,由勾股定理,得![]() ,
,
又∵BF=CE,
∴![]() ,故④正确.
,故④正确.
故选A.
略








