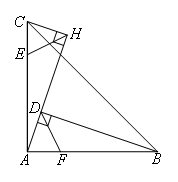
如图,在等腰直角△ABC中,∠BAC=90°,AC=AB,BD⊥AH于D,CH⊥AH于H,HE,DF分别平分
∠AHC和∠ADB.则下列结论中:①△AHC≌△BDA;②DF⊥HE;③DF=HE;④AE=BF.其中正确的结论有( )
- A.①③④
- B.①
- C.①②③
- D.①②③④
答案
正确答案:D
知识点:等腰直角三角形
①∵∠BAC=90°,BD⊥AH,CH⊥AH,
∴∠AHC=∠BDA=90°,
∴∠CAH+∠BAD=90°,∠ABD+∠BAD=90°,
∴∠CAH=∠ABD
又∵AC=AB
∴△AHC≌△BDA(AAS),①正确;
②如图,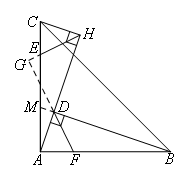
延长BD与AC相交于点M,延长FD,HE交于点G.
∵∠CHD+∠HDM=90°+90°=180°,
∴CH∥BM
∵DF平分∠ADB
∴DG平分∠HDM
又∵HE平分∠AHC
∴∠HGD=90°
∴DF⊥HE,②正确;
③![]()
![]()
又∵∠CHA=∠ADB
∴∠EHA=∠FDB
又∵∠EAH=∠FBD,AH=BD
∴△EHA≌△FDB
∴DF=HE,∴③正确
④∵△EHA≌△FDB
∴AE=BF,④正确.
故选D.
略








