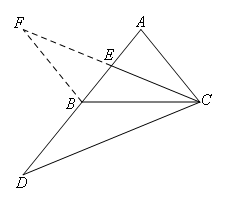
如图,在△ABC中,AB=AC,CE是AB边上的中线,延长AB到D,使BD=AB,连接CD.求证:CD=2CE.

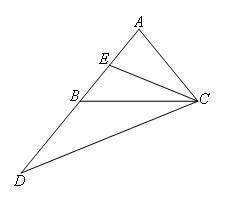
下列辅助线的作法中,能证明CD=2CE的是(    )
①延长CE到点F,使EF=CE,连接AF.

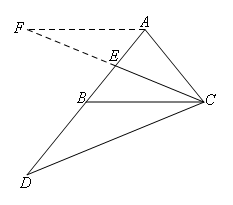
②延长CB到点F,使BF=BC,连接DF.

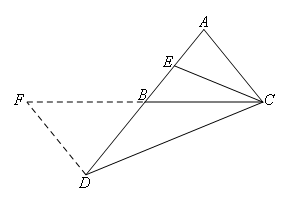
③延长CB到点F,使BF=BC,连接AF.

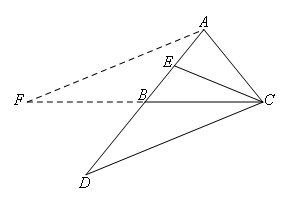
④延长CE到点F,使EF=CE,连接BF.

①结合图中辅助线，可以证明△AEF≌△BEC，
∴AF＝BC，∠FAE＝∠CBE，
∵AB＝AC，
∴∠ABC＝∠ACB，
∴∠FAC＝∠FAE+∠BAC＝∠CBE+∠BAC＝∠ACB+∠BAC＝∠CBD，
∵AC＝AB＝BD，
∴△FAC≌△CBD，
∴CD＝CF＝2CE，故①可以；
②③不能证明；
④结合图中辅助线，可以证明△BEF≌△AEC，
∴BF＝AC，∠FBE＝∠A，
∵AB＝AC，
∴∠ABC＝∠ACB，
∴∠FBC＝∠FBE+∠ABC＝∠A+∠ABC＝∠A+∠ACB＝∠CBD，
∵AC＝AB＝BD＝BF，BC＝BC，
∴△CBF≌△CBD，
∴CD＝CF＝2CE，故④可以；
综上：①④可以．
故选C

略