如图,在直角梯形ABCD中,∠A=90°,∠B=120°,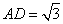
,AB=6.在边AB上取点E,在射线DC上取点F,使得∠DEF=120°.若射线EF经过点C,则AE的长为( )
,AB=6.在边AB上取点E,在射线DC上取点F,使得∠DEF=120°.若射线EF经过点C,则AE的长为( )
- A.2
- B.2或4
- C.2或5
- D.3或5
答案
正确答案：C
知识点：勾股定理 直角梯形 相似三角形的判定与性质
如图，过点C作AB的垂线，垂足为G．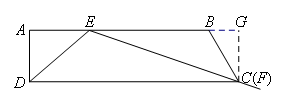
易得∠CBG=60°，
，
∴BG=1，BC=2，CD=AG=AB+BG=7．
若射线EF经过点C（即F与C重合），则△CBE∽△DEC，
∴
，
∴
．
设AE=x，则BE=6-x，EG=7-x，
在Rt△CEG中应用勾股定理得，
，
∴
，
∴
或
，
即AE的长度为2或5．
略
WORD格式（
