如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,∠C=60°,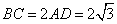 ,点E是BC边的中点.若△DEF是等边三角形,DF交AB于点G,则△BFG的周长为( )
,点E是BC边的中点.若△DEF是等边三角形,DF交AB于点G,则△BFG的周长为( )
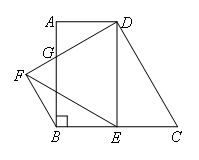
- A.
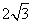
- B.
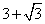
- C.
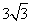
- D.4
答案
正确答案:B
知识点:三角形全等性质与判定 等边三角形的性质 直角梯形
由题意得,![]() .
.
易证四边形ABED为矩形,
∴∠DEC=∠A=90°.
在Rt△CDE中,
∵∠C=60°,
∴![]() .
.
∵△DEF是等边三角形,
∴DF=DE=AB=3,∠AGD=∠EDF=60°,∠ADG=30°.
在Rt△AGD中,![]() ,
,
∴DG=2,FG=DF-DG=1,BG=3-1=2,
∴AG=FG=1,∠AGD=∠FGB,BG=DG=2,
∴△AGD≌△FGB,
∴![]() ,
,
∴△BFG的周长为![]() .
.
略








