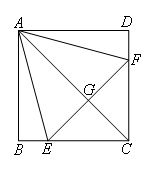
如图，在正方形ABCD中，点E，F分别在BC，CD上，△AEF是等边三角形，连接AC交EF于G．有下列结论：①BE=DF；②∠DAF=15°；③AC垂直平分EF；④BE+DF=EF．其中正确结论有(    )

∵四边形ABCD是正方形，
∴AB=BC=CD=AD，∠B=∠BCD=∠D=∠BAD=90°．
∵△AEF是等边三角形，
∴AE=EF=AF，∠EAF=60°．
∴∠BAE+∠DAF=30°．
在Rt△ABE和Rt△ADF中，

Rt△ABE≌Rt△ADF（HL），
∴BE=DF，①正确．
∠BAE=∠DAF，
∴∠DAF=15°，②正确，
∵BC=CD，
∴BC-BE=CD-DF，即CE=CF，
又∵AE=AF，
∴AC垂直平分EF．③正确．
由△ABE≌△ADF可知
BE=DF，
由③可知
EG=FG，
∵BE≠EG，
∴BE+DF≠EF，④错误
只有三个正确结论，选C

略