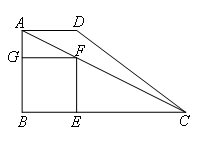
(上接第4题)(2)设正方形 与△ADC重叠部分的面积为S,要求S与t之间的函数关系式,需分 种情况来考虑,时间段的划分应为 .( )
与△ADC重叠部分的面积为S,要求S与t之间的函数关系式,需分 种情况来考虑,时间段的划分应为 .( )
- A.3;
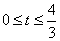 ,
,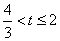 ,
,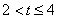
- B.3;
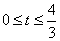 ,
, ,
,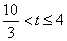
- C.3;
 ,
,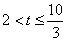 ,
,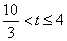
- D.4;
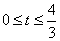 ,
,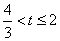 ,
,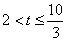 ,
,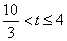
答案
正确答案:D
知识点:图形运动产生的面积问题
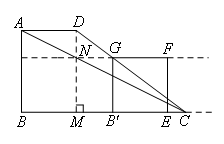
如图,画出正方形![]() 平移的通道,
平移的通道,
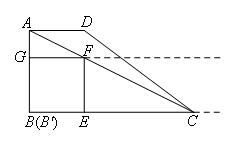
用图形边界碰撞来考虑时间的分段,在四边形![]() 向右平移的过程中:
向右平移的过程中:
点F落在AC上→点F落在CD上→点G落在AC上→点G落CD上→点E与点C重合.
故需分4种情况考虑.
由第(1)问可知整个运动过程中图形平移的距离t的范围是![]() ,只需求出边界碰撞时对应t的取值即可.
,只需求出边界碰撞时对应t的取值即可.
显然点F落在AC上时,t=0;点E与点C重合时,t=4.
①如图,当点F落在CD上时,
过点D作DM⊥BC于点M(点M为点E的起始位置),交直线GF于点N.
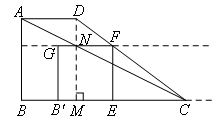
由题意,得四边形ABMD为矩形,AD=BM=2,AB=DM=3,MC=6-2=4.
易证△DMC∽△FEC,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() .
.
②如图,当点G落在AC上时,
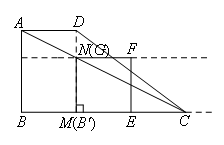
M和![]() 重合,
重合,![]() .
.
③如图,当点G落在CD上时,![]() ,
,
由①易得,![]() ,
,![]() ,
,
∴![]() .
.
综上可得,要求S与t之间的函数关系式,需分4种情况来考虑,时间段的划分应为![]() ,
,![]() ,
,![]() ,
,![]() .
.
略








