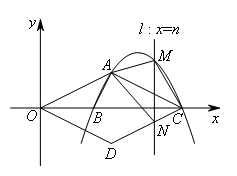
如图，抛物线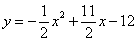与x轴交于B（3，0），C（8，0）两点，
点A（4，2）是抛物线上另一点，连接OA，AC，将△OAC沿x轴翻折后得△ODC．设垂直于x轴的直线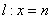与抛物线交于点M，与CD交于点N，若直线沿x轴方向左右平移，且交点M始终位于抛物线上
A，C两点之间，那么四边形AMCN的面积S与n的函数关系式为         ，当S取最大值时，对应的n的值为         ．(    )

• A.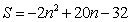，5
• B.，5
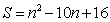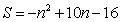• C.，5
• D.，

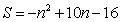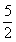
答案

正确答案：C

知识点：二次函数背景下的面积问题  坐标系中的面积问题  铅垂法求面积  

由题意得，点D是由点A沿x轴翻折得到，
∴D（4，-2）．
设直线CD的表达式为y=kx+b，
把C，D两点坐标代入可得，
，
∴，
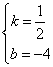∴直线CD的表达式为．
由题意得，点M，N的横坐标均为．
∵点M，N分别在抛物线和直线CD上，
∴，，
∴．
如图，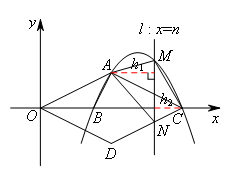






．
当时，S取最大值，此时满足．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>