如图,抛物线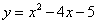 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接BC,已知D(6,7),E(-5,0),点P是第四象限内的抛物线上一点,且∠EDP=∠ABC,则满足题意的点P的坐标为( )
与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接BC,已知D(6,7),E(-5,0),点P是第四象限内的抛物线上一点,且∠EDP=∠ABC,则满足题意的点P的坐标为( )

- A.

- B.
 或
或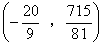
- C.(0,-5)
- D.(0,-5)或(2,-9)
答案
正确答案:A
知识点:二次函数背景下的存在性问题 弦图模型
若在直线ED下方的抛物线上存在一点![]() 满足题意,
满足题意,
则过点D作![]() 的垂线,可以找到点
的垂线,可以找到点![]() ,
,
显然![]() 在直线ED的上方,不在第四象限,不符合题意,
在直线ED的上方,不在第四象限,不符合题意,
故只可能在直线ED下方存在点P.
∵![]() ,
,
∴B(5,0),C(0,-5),
∴△OBC是等腰直角三角形,∠OBC=45°,
即∠ABC=45°.
考虑45°角通常是放在直角三角形中来处理,所以需要构造直角三角形,
而最好的方式是通过定点E作定直线ED的垂线,这样可以利用弦图来解决.
如图,过点E作EF⊥ED交![]() 的延长线于点F,过点E作直线
的延长线于点F,过点E作直线![]() ⊥x轴,过点D作DM⊥
⊥x轴,过点D作DM⊥![]() 于点M,过点F作FN⊥
于点M,过点F作FN⊥![]() 于点N.
于点N.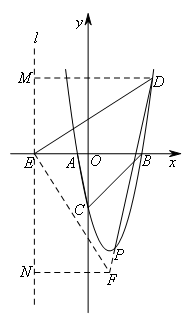
∵∠EDF=45°,ED⊥EF,
∴△DEF是等腰直角三角形.
由弦图模型可知△DME≌△ENF,
∴DM=EN,ME=NF.
∵D(6,7),E(-5,0),
∴F(2,-11),
∴直线![]() :
:![]() ,
,
联立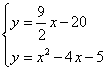 ,解得
,解得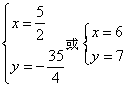 ,
,
∴![]() .
.
∴符合题意的点P的坐标为![]() .
.
略








