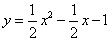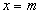已知抛物线与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，直线与x轴交于点D．在第一象限内，若直线上存在点P，使得以P，B，D为顶点的三角形与△OBC全等，则点P的坐标为(    )

由题意得，A（-1，0），B（2，0），C（0，-1），
∴OB=2，OC=1．
点O，B，C为定点，△OBC为目标三角形，直角边长分别为2和1．
直线与x轴垂直，点D是直线与x轴的交点，点P是直线上的动点，
这时确定了∠PDB为直角，
要使得以P，B，D为顶点的三角形与△OBC全等，
只需BD，PD和△OBC两直角边的长度相等即可．
点B为定点，从BD长度入手确定直线的位置，
再根据PD的长度确定点P的坐标．
如图，当BD=BO=2时，m=4．

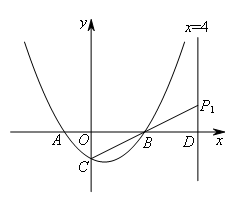
由，得点的坐标为（4，1）．
如图，当BD=OC=1时，m=3或1．

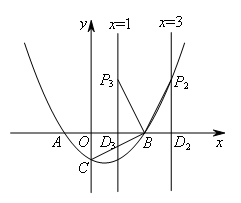
由DP=OB=2，得，．
综上得，点P的坐标为（4，1），（3，2）或（1，2）．

略