如图,在平面直角坐标系xOy中,直线y=x+4与x轴、y轴分别交于点A,B,D为线段AB上一动点,过点D作x轴的垂线,垂足为点C,CD的延长线交抛物线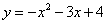 于点E,连接BE.
于点E,连接BE.
若△DBE和△DAC相似,则点D的坐标为( )
- A.
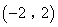
- B.
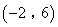
- C.
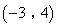 或
或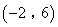
- D.
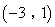 或
或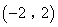
答案
正确答案:D
由题意得,![]() ,
,![]() ,OA=OB,
,OA=OB,
∴△AOB是等腰直角三角形,∠BAO=45°.
∵CD⊥x轴于点C,
∴△DAC为等腰直角三角形.
要使得△DBE和△DAC相似,△DBE需为等腰直角三角形.
对于△DBE来说,点B是定点,点D,E均为动点,
且易知∠EDB=45°,要使得△DBE为等腰直角三角形,需从直角出发进行分类讨论.
如图,当点E为直角顶点时,BE∥AO,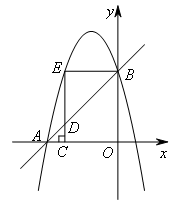
此时点E的纵坐标为4,代入二次函数表达式可得点E的坐标为(-3,4),
∴![]() ,
,
∴![]() .
.
如图,当点B为直角顶点时,BE⊥AB.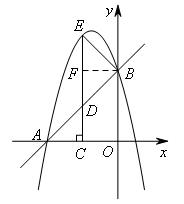
由直线AB的斜率为1可知直线BE的斜率为-1,
结合点B的坐标(0,4),可求得直线BE的表达式为y=-x+4.
由![]() 得,
得,![]() ,
,
∴点E的坐标为(-2,6),
∴![]() ,
,
∴![]() .
.
综上得,点D的坐标为(-3,1)或(-2,2).
略








