如图，抛物线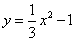与x轴正半轴交于点A，与y轴交于点B．P是经过点B的直线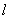上一点，当直线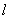绕点B任意旋转时（不与坐标轴平行或重合），若在直线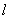上存在点P，使得△PAB与
△AOB相似（相似比不为1），则这样的直线共有(    )条．

先确定点P的位置，再确定直线．
从分析定点、动点出发，点A，O，B均为定点，点P是动点，
目标△AOB是固定的三角形，先研究清楚△AOB的性质，再去和△PAB对应．
由题意得，，，
∴，OB=1，
∴∠OAB=30°，即△AOB是含30°角的直角三角形．
∵△PAB与Rt△AOB相似，且相似比不为1，
∴△PAB是直角三角形，两锐角分别为30°和60°．
以直角顶点进行分类．
如图，当点B为直角顶点时，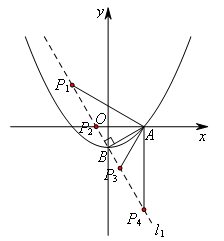

过点B作AB的垂线，点P在直线上，分别使∠BAP=30°或60°，
△PAB共有四种情况，均符合要求，直线满足题意．
如图，当点A为直角顶点时，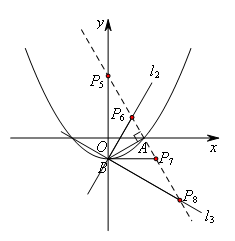

过点A作AB的垂线，点P在这条垂线上，分别使∠ABP=30°或60°，
△PAB共有四种情况，符合要求的是和，
即点B，所在的直线和点B，所在的直线满足题意．
当点P为直角顶点时，AB为Rt△PAB的斜边，
此时易得△PAB和△AOB全等，不符合题干要求．
综上得，满足题意的直线共有3条．

略