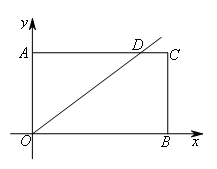
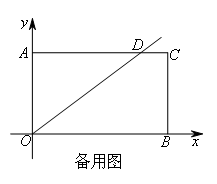
如图，长方形AOBC的顶点O在坐标原点，边OB，OA分别在x轴、y轴的正半轴上，且
OA=6，OB=10，射线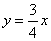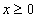（）交线段AC于点D．动点P从点O出发，以每秒2个单位长度的速度沿
O→A→D→O的路线匀速运动，同时点Q也从点O出发，以每秒1个单位长度的速度沿OB向终点B运动，当其中一点到达终点时，另一点也随之停止运动．设运动的时间为t秒，则△OPQ的面积S与t之间的函数关系式为(    )

• A.
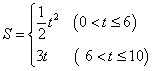
• B.
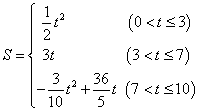
• C.
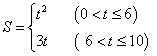
• D.

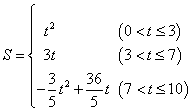
答案

正确答案：D

知识点：一次函数之动点问题  

∵的斜率为，OA=6，
∴AD=8，
∴OD=10．
研究动点的运动情况，确定运动的时间范围为．
①当时，画出符合题意的图形，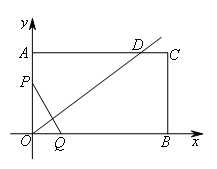

∵OP=2t，OQ=t，
∴．
②当时，画出符合题意的图形，

∵OQ=t，
∴．
③当时，画出符合题意的图形，

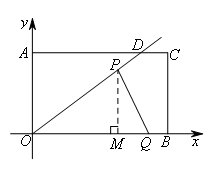
∵OQ=t，OP=24-2t，
∴．
综上，答案选D．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>