如图1，在长方形ABCD中，点E在AD边上，且BE=2AE．分别以BE，CE为折线，将A，D向BC的方向折过去，如图2所示．若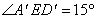，则∠BCE的度数为(    )

1．思路点拨：
遇到折叠问题首先要理解折叠变换是一种全等变换，利用折叠可以转移边、转移角．
通常的思考角度是：先找折痕；折痕两侧的图形是全等图形，由此进行转移和表达；
最后结合条件建方程求解．
2．解题过程：
在Rt△ABE中，BE=2AE，
∴∠ABE=30°，∠AEB=60°．
由折叠的性质可知，，，
∵∠AEB=60°，，
∴，
∴，
∴，．
∵AD∥BC，
∴∠BCE=∠DEC=37.5°．
故选D．
3．易错点：
①不能发现含30°角的直角三角形；
②利用折叠转移角度之后，不能借助平行和所求目标建立联系．

略