将长方形纸片ABCD沿过点B的直线折叠，使点A落在BC边上的点F处，折痕为BE
（如图1）；再沿过点E的直线折叠，使点D落在BE边上的点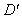处，折痕为EG（如图2）；再展平纸片（如图3），则图3中tanα的值为(    )

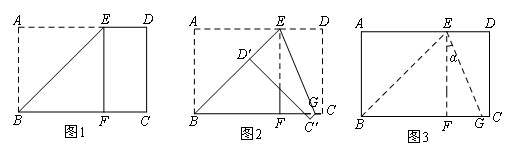
• A.
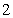
• B.
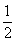
• C.
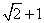
• D.

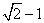
答案

正确答案：D

知识点：数形结合思想  翻折变换(折叠问题)  

由题意，得∠EBF=∠BEF=45°，∠BED=135°，
由折叠性质，得，
∴∠α=22.5°．
在△BEG中，∠EGB=180°-45°-67.5°=67.5°，
∴BE=BG．
设BF=EF=x，则，
∴．
在Rt△EFG中，tanα=tan22.5°=．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>