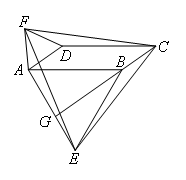
如图，在平行四边形ABCD中，分别以AB，AD为边向外作等边三角形ABE和
等边三角形ADF，延长CB交AE于点G，点G在点A，E之间，连接CE，CF，EF，有下列四个结论：
①△CDF≌△EBC；②∠CDF=∠EAF；③△ECF是等边三角形；④CG⊥AE．其中一定正确的是(    )

①∵四边形ABCD是平行四边形，
∴AD=BC，DC=AB，∠ADC=∠ABC．
∵△ADF，△ABE均为等边三角形，
∴∠ADF=∠ABE=60°，AD=DF=BC，AB=BE=DC，
∴∠FDC=∠CBE，
∴△CDF≌△EBC．
故结论①正确．
②易证△CDF≌△EAF，
∴∠CDF=∠EAF．
故结论②正确．
③由①②可得，
△CDF≌△EBC≌△EAF，
∴CF=EC=EF，
∴△ECF是等边三角形．
故结论③正确．
④若CG⊥AE，则G是AE的中点，∠ABG=30°，∠ABC=150°，
题目缺少这个条件，故CG⊥AE不一定成立．即结论④不一定正确．
故选B．

略