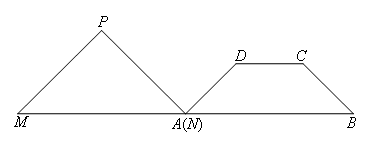
如图，在等腰梯形ABCD中，AB∥DC，∠DAB=45°，AB=10，CD=4．等腰直角三角形PMN的斜边MN=10，点A与点N重合，MN与AB在同一条直线上．等腰梯形ABCD不动，等腰直角三角形PMN沿AB所在直线以每秒1个单位长度的速度向右匀速运动，直到点N与点B重合为止．设运动的时间为x（s）
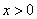（），等腰直角三角形PMN与等腰梯形ABCD重叠部分的面积为y．

（1）在整个运动过程中，当点D落在PN上时，运动的距离为(    )

• A.
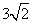
• B.6
• C.4
• D.

答案

正确答案：B

知识点：等腰直角三角形  等腰梯形的性质  图形运动产生的面积问题  

图形运动产生的面积问题，第一步需要研究基本图形，需要把运动图形跟运动背景结合起来进行对比研究，也就是需要把△PMN和等腰梯形ABCD研究清楚．
如图，过点D作DE⊥AB于点E，过点C作CF⊥AB于点F，各线段长如图所示，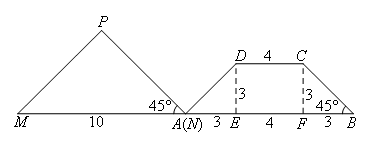

容易发现，PN∥CB，PM∥AD．
当点D落在PN上时，如图所示，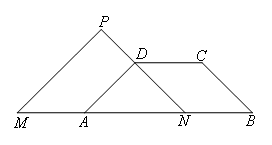

四边形DNBC是平行四边形，
∴BN=CD=4，
∴AN=AB-BN=10-4=6，
即运动的距离为6．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>