如图,直线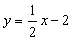 与x轴、y轴分别交于点A,C,过A,C两点的抛物线与x轴交于另一点B(1,0).D为直线AC上方的抛物线上一动点,连接DA,DC,当△DAC的面积最大时,点D的坐标为( )
与x轴、y轴分别交于点A,C,过A,C两点的抛物线与x轴交于另一点B(1,0).D为直线AC上方的抛物线上一动点,连接DA,DC,当△DAC的面积最大时,点D的坐标为( )
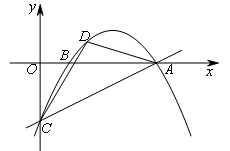
- A.
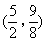
- B.(2,1)
- C.(3,1)
- D.
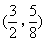
答案
正确答案:B
知识点:坐标系中的面积问题 铅垂法求面积 面积处理思路(割补法)
要求当△DAC的面积最大时,对应的点D的坐标,
需先表达出△DAC的面积,再利用函数的性质解决问题.
点D为直线AC上方的抛物线上一动点,A,C为定点,利用铅垂法表达△DAC的面积.
由题意得,C(0,-2),A(4,0).
设抛物线的解析式为![]() ,
,
将C(0,-2)代入可得,![]() ,
,
∴![]() .
.
如图,过点D作DE∥y轴,交AC于点E.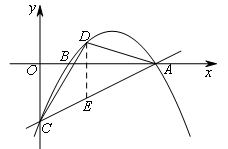
![]() .
.
设点D的横坐标为m(![]() ),
),
则![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴当![]() 时,
时,![]() 最大,
最大,
此时点D的坐标为(2,1).
略








