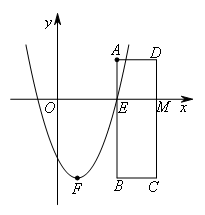
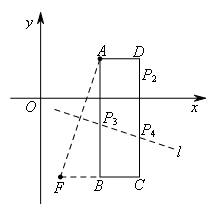
如图,在矩形ABCD中,已知A(3,2),B(3,-4),C(5,-4),点E是直线AB与
x轴的交点,抛物线 过点E,且顶点F的横坐标为1,点M是直线CD与x轴的交点.若P是
过点E,且顶点F的横坐标为1,点M是直线CD与x轴的交点.若P是
矩形ABCD边上的一点,且△AFP是等腰三角形,则点P的坐标为( )
- A.
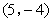 ,
,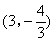 ,
,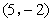
- B.
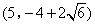 ,
,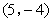 ,
,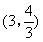 ,
,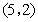
- C.
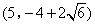 ,
,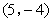 ,
,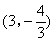 ,
,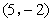
- D.
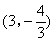 ,
,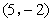
答案
正确答案:C
知识点:等腰三角形的存在性(两定一动)
1.解题要点
①首先根据题意确定抛物线的解析式,进而求出点F的坐标,可以得到F,B,C三点在同一条直线上;
②分析目标△AFP,A,F是定点,P是动点,符合“两定一动”的特征,可以借助两圆一线来解决问题;
③抛物线在等腰三角形存在性的分析中,没有发挥作用,属于干扰图形,画图分析时,可以直接去掉,而三点F,B,C共线,可以在图中直接标出.
2.解题过程
由题意得,![]() ,
,![]() ,
,
∴a=1,b=-2,
∴![]() ,
,
∴![]() .
.
连接AF,易求![]() ,
,
![]() .
.
当AF为等腰三角形AFP的腰时,
①以点A为圆心,AF长为半径作圆,交矩形ABCD的边于点![]() ,如图所示,
,如图所示,
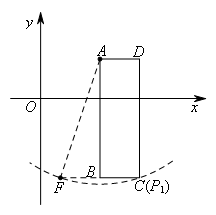
容易证明,点![]() 与点C重合,
与点C重合,
∴![]() .
.
②以点F为圆心,AF长为半径作圆,交矩形ABCD的边于点![]() ,如图所示,
,如图所示,
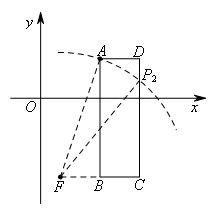
连接![]() ,则
,则![]() ,
,
在![]() 中,由勾股定理可求
中,由勾股定理可求![]() ,
,
∴![]() .
.
当AF为等腰三角形AFP的底边时,作AF的垂直平分线![]() 交矩形ABCD的边于点
交矩形ABCD的边于点![]() ,如图所示,
,如图所示,
易求![]() ,
,
∴![]() ,
,![]() .
.
综上,符合题意的点P的坐标为![]() ,
,![]() ,
,![]() ,
,![]() .
.
略








