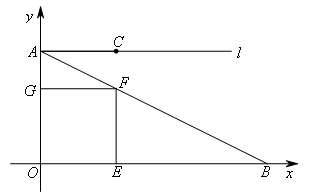
如图,在平面直角坐标系xOy中,已知A(0,3),B(6,0),过点A的射线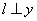 轴,C是射线
轴,C是射线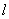 上一点,且点C的横坐标为2.正方形OEFG的顶点F落在线段AB上,边OE落在x轴上,边OG落在y轴上,将正方形OEFG沿OB向右平移,记平移中的正方形OEFG为正方形DEFG,正方形DEFG的边EF与AB交于点M,连接CD,DM,CM.设平移的距离为
上一点,且点C的横坐标为2.正方形OEFG的顶点F落在线段AB上,边OE落在x轴上,边OG落在y轴上,将正方形OEFG沿OB向右平移,记平移中的正方形OEFG为正方形DEFG,正方形DEFG的边EF与AB交于点M,连接CD,DM,CM.设平移的距离为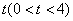 ,当△CDM是直角三角形时,t的值为( )
,当△CDM是直角三角形时,t的值为( )
- A.
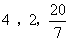
- B.
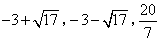
- C.
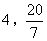
- D.
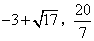
答案
正确答案:D
知识点:直角三角形的存在性
1.解题要点
①首先研究基本图形,△AOB是三边之比为![]() 的直角三角形,正方形
的直角三角形,正方形![]() 的边长为2,各线段长如图所示,
的边长为2,各线段长如图所示,
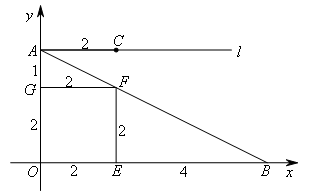
②分析运动状态,对起点、终点进行判断,能够得到当点E平移到点B时,运动停止;
③画出草图,如图所示,

分析目标△CDM,D,M都是动点,C是定点,若△CDM是直角三角形,需要根据直角顶点进行分类,把三个顶点轮流作直角顶点进行分析;
④由于此题中,当点C和点D为直角顶点时,图形不容易画出,且表达线段或者斜率时会牵涉到正负的问题,所以采取表达三边长,利用勾股定理逆定理的方式来解决问题.
2.解题过程
由题意得,OD=t,DB=6-t,EB=4-t,
∴D(t,0).
∵△AOB∽△MEB,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵C(2,3),
∴![]() ,
,
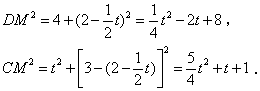
①当点C为直角顶点时,![]() ,
,
即![]() ,此方程无解.
,此方程无解.
②当点M为直角顶点时,![]() ,
,
即![]() ,解得
,解得![]() .
.
∵![]() ,
,
∴![]() .
.
③当点D为直角顶点时,![]() ,
,
即![]() ,解得
,解得![]() ,符合题意.
,符合题意.
综上所述,符合题意的t的值为![]() .
.
略








