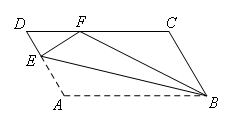
如图，在平行四边形ABCD中，点E在AD边上，以BE为折痕，将△ABE向上翻折，点A恰好落在CD边上的点F处．若△FDE的周长为8，△FCB的周长为22，则FC的长为(    )

如图，由折叠性质知，FE=AE，BF=BA．

∵FD+DE+FE=8，FC+CB+BF=22，
∴FD+DE+AE=8，即FD+AD=8①，
同理FC+CB＋BA=22，即FC+AD+CD=22②．
②-①得，FC+CD-FD=14，
又∵CD=FC+FD，
∴FC+FC=14，
∴FC=7，故选B．

略