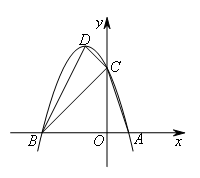
如图,抛物线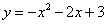 与x轴交于A,B两点(点A在点B的右侧),与y轴交于点C,D为抛物线的顶点.若P为坐标轴上一点,要使△PAC与△BCD相似,则点P的坐标为( )
与x轴交于A,B两点(点A在点B的右侧),与y轴交于点C,D为抛物线的顶点.若P为坐标轴上一点,要使△PAC与△BCD相似,则点P的坐标为( )
- A.
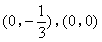
- B.

- C.
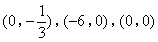
- D.
答案
正确答案:D
1.解题要点
①分析基本图形,求出A,B,C,D的坐标,进行标注,
△AOC是两直角边之比为1:3的直角三角形.
②从边角入手分析目标△BCD,是一个固定的直角三角形,且两直角边之比为1:3;
△PAC中,A,C是定点,P是动点;
若两个三角形相似,需要保证△PAC是直角三角形,且两直角边之比为1:3.
③画出符合题意的图形,结合△AOC的形状进行分析,求出点P的坐标.
2.解题过程
由题意得,![]() ,
,
∴△BOC是等腰直角三角形,![]() ,∠BCO=45°.
,∠BCO=45°.
如图,过点D作DE⊥y轴于点E.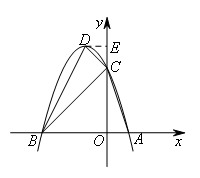
则DE=CE=1,
∴△EDC是等腰直角三角形,![]() ,∠DCE=45°,
,∠DCE=45°,
∴∠BCD=90°,![]() .
.
若△PAC与△BCD相似,需要保证△PAC是直角三角形,且两直角边之比为1:3.
①当点A为直角顶点时,如图,过点A作![]() 交y轴于点
交y轴于点![]() .
.
容易证明![]() ∽△OCA,
∽△OCA,
∵△OCA是两直角边之比为1:3的直角三角形,
∴点![]() 满足题意,
满足题意,
由![]() 可求得点
可求得点![]() .
.
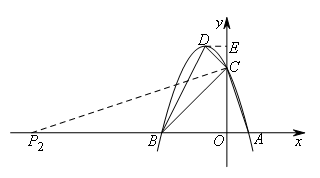
②当点C为直角顶点时,如图,过点C作![]() 交x轴于点
交x轴于点![]() .
.
同①可证点![]() 满足题意,
满足题意,
由![]() 可求得点
可求得点![]() .
.
③当点P为直角顶点时,以AC为直径作圆,交坐标轴于点![]() ,易知点
,易知点![]() 与点O重合,
与点O重合,
∴![]() .
.
综上,符合条件的点P的坐标为![]() ,
,![]() ,
,![]() .
.
略








