(上接第4题)(2)对于(1)中的抛物线,点M是直线AB上方的抛物线上一动点,过点M作MN⊥x轴于点N,若△AMN与△ACD相似,则点M的坐标为( )
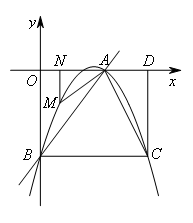
- A.
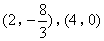
- B.
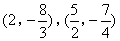
- C.
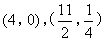
- D.
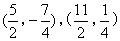
答案
正确答案:D
知识点:相似三角形的存在性
1.解题要点
①研究目标△ACD,AD=4,CD=8,△ACD是两直角边之比为1:2的直角三角形;
△AMN中,A是定点,M,N是动点,∠ANM=90°属于不变特征,
若两个三角形相似,只需满足![]() .
.
②由于点M可落在x轴上方,也可落在x轴下方,
表达线段长时,会有所不同,需要分类讨论.
③分类画图,表达,利用①中的关系建等式.
2.解题过程![]() ,
,
设点M的坐标为![]() ,
,![]() .
.
①当![]() 时,如图所示,
时,如图所示,
![]() .
.
当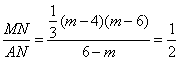 时,解得
时,解得![]() ,
,
∴![]() .
.
当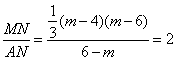 时,解得
时,解得![]() ,不符合题意,舍去.
,不符合题意,舍去.
②当![]() 时,如图所示,
时,如图所示,
![]() .
.
当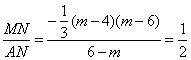 时,解得
时,解得![]() ,
,
∴![]() .
.
当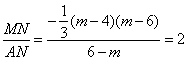 时,解得
时,解得![]() ,不符合题意,舍去.
,不符合题意,舍去.
综上,符合题意的点M的坐标为![]() .
.
略







