把Rt△ABC和Rt△DEF按图1所示方式摆放（点C与点E重合），点B，C（E），F在同一条直线上，∠ACB=∠EDF=90°，∠DEF=45°，AC=8cm，BC=6cm，EF=9cm．如图2，△DEF从图1所示的位置出发，以1cm/s的速度沿CB向左匀速移动，同时，动点P从点B出发，以2cm/s的速度沿BA向点A匀速移动．当△DEF的顶点D移动到AC边上时，△DEF和点P同时停止移动．设移动时间为t（s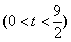），DE与AC相交于点Q，连接PQ．

（1）当点A在线段PQ的垂直平分线上时，t的值为(    )

• A.2
• B.4
• C.1
• D.3

答案

正确答案：A

知识点：动点处理框架  图形运动处理框架  

1．解题要点
①首先研究基本图形，可得AB=10cm，Rt△ABC的三边之比为3：4：5，
Rt△DEF和Rt△CEQ都是等腰直角三角形．
②分析运动状态，画出通道，设点D落在AC上时的对应点为H，
那么点P，D的运动状态如图所示，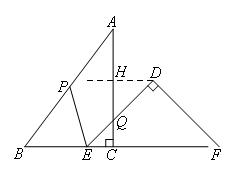



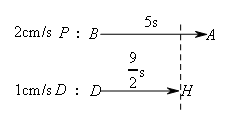
此时，BP=2t，CQ=CE=t．
③从动点运动表达入手，利用垂直平分线的性质（垂直平分线上的点到线段两端点的距离相等），建立等式求解．
2．解题过程
若点A在线段PQ的垂直平分线上，
则AP=AQ．
由题意得AB=10cm，AC=8cm，BP=2t，CQ=t，
∴AP=10-2t，AQ=8-t，
∴10-2t=8-t，
∴t=2．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>