如图,在平行四边形ABCD和平行四边形BEFG中,AB=AD,BG=BE,点A,B,E在同一直线上,P是线段DF的中点,连接PG,PC.若∠ABC=∠BEF=60°,则PG:PC的值为( )
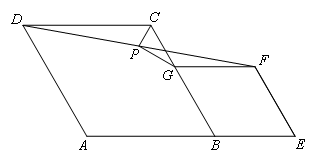
- A.
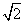
- B.
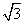
- C.
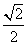
- D.
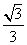
答案
正确答案:B
思考方向:平行+中点,可考虑类倍长中线.
如图,延长GP交CD于点H.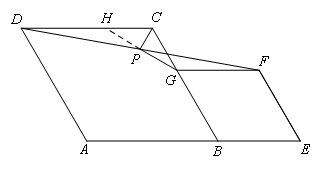
由DC∥FG,P是DF中点,可证△PHD≌△PGF(AAS),
则DH=FG,PH=PG.
在平行四边形ABCD中,AB=AD,
∴四边形ABCD是菱形,
∴CD=CB.
同理,四边形BEFG是菱形,FG=GB,
∴DH=GB,
∴CH=CG,△HCG是等腰三角形,
∴CP⊥PG,∠PCG=![]() ∠DCB.
∠DCB.
在菱形ABCD中,∠ABC=60°,
∴∠DCB=120°,
∴∠PCG=60°,
∴在Rt△PCG中,![]() .
.
故选B.
略








