如图,P为正方形ABCD内一点,连接PA,PB,过点P作PE⊥CD于点E.若PA=PB=PE,
且AB=16,则PA的长为( )

- A.
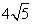
- B.10
- C.8
- D.12
答案
正确答案:B
思考方向:由PE⊥CD,可以考虑将垂线打通,构造矩形.
如图,延长EP交AB于点F,
可得四边形BCEF是矩形,BC=EF,PF⊥AB.
又PA=PB,得等腰三角形APB中,AF=BF.
在正方形ABCD中,AB=BC=EF=16,
则AF=BF=8,
设PA=x,则PE=x,PF=16-x.
在Rt△APF中,由勾股定理,得![]() ,
,
解得,![]() ,
,
即PA=10.
故选B.
略








