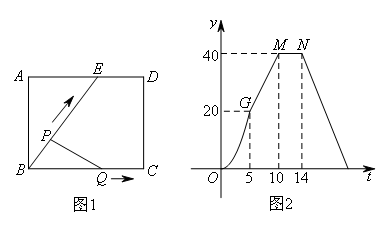
如图1所示,E为矩形ABCD的边AD上一点,动点P,Q同时从点B出发,点P以1cm/s的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/s的速度沿BC运动到点C时停止.设点P出发t s时,△BPQ的面积为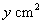 .已知y与t之间的函数关系如图2所示(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:①当
.已知y与t之间的函数关系如图2所示(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:①当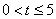 时,
时,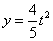 ;②当t=6时,△ABE≌△PQB;③
;②当t=6时,△ABE≌△PQB;③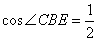 ;④当
;④当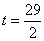 时,△ABE∽△QBP.其中正确的是( )
时,△ABE∽△QBP.其中正确的是( )
- A.①②
- B.①③④
- C.③④
- D.①②④
答案
正确答案:D
结合图1、图2分析点P,Q的运动状态: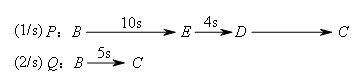
由题意可知,当t=5时,点Q到达点C处,当t=10时,点P到达点E处.
∵点P运动的速度为1cm/s,点Q运动的速度为2cm/s,
∴BC=BE=10.
∵四边形ABCD为矩形,
∴AD=BC=10,AB=CD.
∵点P从点E运动到点D所用时间为4s,
∴DE=4,AE=6.
在△ABE中由勾股定理得,AB=8,
∴CD=8.
①当![]() 时,点P在BE上运动.
时,点P在BE上运动.
如图,过点P作PF⊥BC于点F.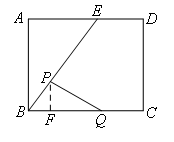
则△PBF∽△BEA,![]() .
.
由题意得,BP=t,BQ=2t,
∴![]() .
.
故①正确.
②当t=6时,点P在BE上,且BP=6,点Q与点C重合,如图所示,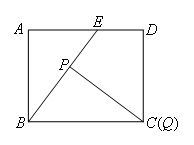
∵AD∥BQ,
∴∠BEA =∠QBP.
又∵AE=BP=6,BQ=BE=10,
∴△ABE≌△PQB.
故②正确.
③∵∠CBE=∠BEA,
∴cos∠CBE= cos∠BEA.
在Rt△ABE中,![]() .
.
故③错误.
④当![]() 时,点P在CD上,点Q与点C重合,如图所示,
时,点P在CD上,点Q与点C重合,如图所示,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵∠A=∠Q=90°,
∴△ABE∽△QBP.
故④正确.
综上得,答案选D.
略








