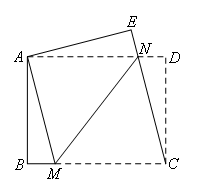
如图,在矩形ABCD中, ,将矩形ABCD折叠,使点C与点A重合,点D落在点E处,折痕为MN,连接CN.若△CDN的面积与△CMN的面积之比为1:4,则
,将矩形ABCD折叠,使点C与点A重合,点D落在点E处,折痕为MN,连接CN.若△CDN的面积与△CMN的面积之比为1:4,则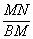 的值为( )
的值为( )
- A.2
- B.4
- C.
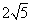
- D.
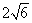
答案
正确答案:D
知识点:勾股定理 矩形的性质 翻折变换(折叠问题)
∵△CDN的面积与△CMN的面积之比为1:4,
∴DN:CM=1:4.
设DN=x,则CM=4x.
由折叠得,∠ANM=∠CNM,CN=AN.
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∴∠ANM=∠CMN,
∴∠CMN=∠CNM,
∴CM=CN=AN=4x,
∴BM=DN=x.
∵AN∥CM,
∴四边形AMCN是平行四边形,
∴AM=CN=4x.
在Rt△ABM中,由勾股定理得,![]() .
.
如图,过点M作MF⊥AD于点F.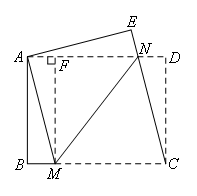
则![]() .
.
在Rt△MFN中,由勾股定理得,![]() ,
,
故![]() .
.
略








