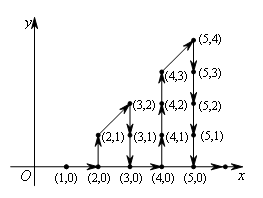
如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“→”方向排列，如（1，0），（2，0），（2，1），（3，2），（3，1），（3，0）（4，0），…，根据这个规律探索可得，第100个点的坐标为(    )

首先确定第100个点的横坐标，再来确定纵坐标．
通过点的个数容易发现，每一列点的个数都和该列点的横坐标相同（即横坐标为n的那一列有n个点）．
∵1+2+3+…+14=105，1+2+3+…+13=91，
∴第100个点的横坐标为14，
由图可知第105个点在第14列的最上方，第91个点在第13列的最下方．
对于每一列，从上往下，纵坐标依次减小1，
第14列共14个点，从上往下的纵坐标依次是13（第105个点），12（第104个点），
11（第103个点），10（第102个点），9（第101个点），8（第100个点）……
∴第100个点的坐标为（14，8）．

略