（上接第1题）（2）方法迁移：
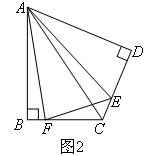
如图2，将Rt△ABC沿斜边翻折得到△ADC，E，F分别为边CD，BC上的点，且满足．则DE，BF，EF之间的数量关系为(    )

点击查看解析视频：http://v.xxt.cn/course/video.do?id=13002
1．解题要点
①照搬（1）中的思路：辅助线描述；△ADE≌△ABG；∠GAF=∠EAF；△AGF≌△AEF．
②辅助线同样是：延长CB到G，使得BG=DE，连接AG．
③能够按照①中的框架操作的关键特征在于：AB=AD，∠ABC+∠ADC=180°，能够实现旋转，即能够得到△ADE≌△ABG；
，能够保证△AGF≌△AEF．
不变特征是：AB=AD，∠ABC+∠ADC=180°，．
2．解题过程
如图，延长CB到G，使得BG=DE，连接AG．

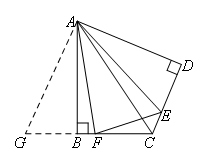
∵△ADC是由Rt△ABC沿斜边AC翻折得到的，
∴AB=AD，∠ABC=∠ADC=90°．
∵BG=DE，
∴△ADE≌△ABG，
∴AG=AE，∠GAB=∠EAD．
∵，
∴∠BAF+∠EAD=∠EAF，
∴∠BAF+∠GAB=∠EAF，
∴∠GAF=∠EAF，
∴△AGF≌△AEF，
∴EF=GF=BG+BF，
∴DE+BF=EF．

略