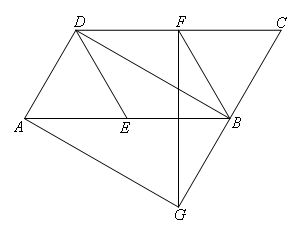
已知如图，在平行四边形ABCD中，E，F分别为边AB，CD的中点，BD是对角线，AG∥DB，
交CB的延长线于点G，连接GF，若AD⊥BD．下列结论：
①DE∥BF；②四边形BEDF是菱形；③FG⊥AB；④．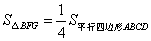
其中正确的是（    ）

①在平行四边形ABCD中，
AB∥CD，AB=CD，
又∵E，F分别为边AB，CD的中点，
∴BE=DF，
∴四边形BEDF为平行四边形，
∴DE∥BF，①正确；
②由①知四边形BEDF为平行四边形，
∵AD⊥BD，E为边AB的中点，
∴DE=BE=AE，
∴四边形BEDF是菱形，②正确；
③∵AG∥DB，AD∥BG，
∴四边形ADBG是平行四边形，
又∵AD⊥BD
∴四边形ADBG为矩形，
∴AD=BG=BC，
若FG⊥AB，则BF=BC=BG，
不能证明BF=BC，即FG⊥AB不恒成立，③不正确．
④由③知BC=BG
∴，
∵F为CD中点，
∴，
∴，
故④正确．
综上，①②④正确．
故选D．

略