如图,在平行四边形ABCD中,∠ABD=30°,AB=4,AE⊥BD于E,CF⊥BD于F,且E,F恰好是BD的三等分点,M,N分别是AB,CD的中点,那么四边形MENF的面积是( )
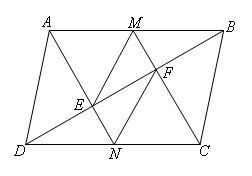
- A.
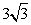
- B.
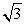
- C.
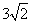
- D.
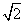
答案
正确答案:B
知识点:平行四边形的性质
思考方向:猜测四边形MENF是平行四边形,已经有一组对边平行了(MF∥NE),
只需证明相等即可.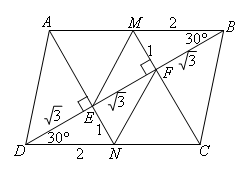
如图,在平行四边形ABCD中,AB∥CD,AB=CD
∵M,N是AB,CD的中点,AB=4
∴BM=2,DN=2
在Rt△MBF中,∠MBF=30°
∴MF=![]() =1,BF=
=1,BF=![]() =
=![]()
同理,EN=![]() =1,DE=
=1,DE=![]() =
=![]()
∴MF=NE
∵MF⊥BD,NE⊥BD
∴MF∥NE
∴四边形MENF是平行四边形
∵E,F是BD的三等分点
∴DE=EF=FB
∴EF=![]()
∴![]()
故选B.
略








