如图,在△ABC中,点E,D,F分别在边AB,BC,AC上,且DE∥AC,DF∥AB.下列四个结论中,不正确的是( )
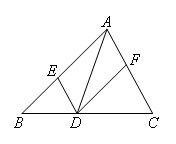
- A.四边形AEDF是平行四边形
- B.如果∠BAC=90°,那么四边形AEDF是矩形
- C.如果AD平分∠BAC,那么四边形AEDF是菱形
- D.如果AD⊥BC,那么四边形AEDF是菱形
答案
正确答案:D
选项A:
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
则A选项正确,不符合题意.
选项B:
若∠BAC=90°,∵四边形AEDF是平行四边形,
∴四边形AEDF是矩形,
则B选项正确,不符合题意.
选项C:
∵AD平分∠BAC,
可证得AE=DE.
又∵四边形AEDF是平行四边形,
∴四边形AEDF是菱形,
则C选项正确,不符合题意.
选项D:
AD⊥BC,不能判定四边形AEDF是菱形,
则D选项错误,符合题意.
故选D.
略








