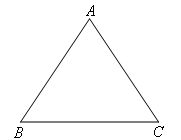
如图,在△ABC中,AB=AC,BC=4,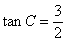 ,如果将△ABC沿直线
,如果将△ABC沿直线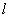 翻折后,点C落在AB边的中点处,直线
翻折后,点C落在AB边的中点处,直线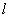 与BC边交于点D,那么BD的长为 .
与BC边交于点D,那么BD的长为 .
- A.
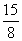
- B.
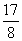
- C.
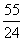
- D.
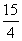
答案
正确答案:B
知识点:轴对称的性质 翻折变换(折叠问题)
1.解题要点
①此题在河南中考数学试卷中处于第15题的位置,为最后一个填空题.
②13~15题常与平移、旋转、折叠(轴对称)等操作结合起来进行考查,有时需要分类讨论,综合性较高.
考查点:几何综合、函数综合、求不规则图形面积、规律探究.
2.解题过程
如图,记AB的中点为M,分别过点A,M作BC的垂线,垂足分别为点E,F.连接MD.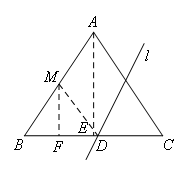
由折叠得,CD=MD.
∵AB=AC,AE⊥BC,BC=4,
∴∠B=∠C,BE=CE=2,
∴![]() .
.
∵M是AB边的中点,MF⊥BC,
∴F是BE的中点,BF=EF=1.
在Rt△BMF中,![]() ,
,
∴![]() .
.
设BD=x,则MD=CD= 4-x,DF=x-1,
在Rt△MDF中,由勾股定理得,![]() ,
,
即![]() ,
,
解得![]() ,即BD的长为
,即BD的长为![]() .
.
略








