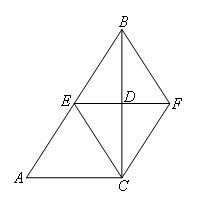
如图，在△ABC中，∠ACB=90°，BC的垂直平分线EF交BC于点D，交AB于点E，
且BE=BF，添加一个条件，仍不能证明四边形BECF为正方形的是(    )

∵EF垂直平分BC，
∴BE=CE，BF=CF．
∵BE=BF，
∴BE=CE=BF=CF．
∴四边形BECF是菱形．
①当BC=AC时，∠ACB=90°，
∴∠EBC=45°．
∴∠EBF=2∠EBC=90°．
∴菱形BECF是正方形．
故选项A不符合题意；
②当CF⊥BF时，菱形BECF是正方形，
故选项B不符合题意；
③当BD=DF时，BC=EF，
∴菱形BECF是正方形．
故选项C不符合题意；
④当AC=BF时，无法得出菱形BECF是正方形，故选项D符合题意．
故选D.

略