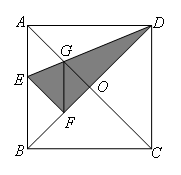
如图,在正方形纸片ABCD中,对角线AC,BD相交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB,AC于点E,G,连结GF.下列结论:
①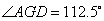 ;②
;②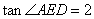 ;③
;③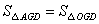 ;④四边形
;④四边形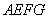 是菱形;
是菱形;
⑤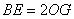 .则其中正确的是( )
.则其中正确的是( )
- A.①②③
- B.①②④
- C.③④⑤
- D.①④⑤
答案
正确答案:D
①由∠DAG=45°,∠ADE=22.5°,
可得∠AGD=112.5°.①正确.
②若tan∠AED=2,则AD=2AE.
因为AD=AB,所以AE=BE.
又因∠ADE=∠BDE,
所以△ADE为等腰三角形,与AD=BD矛盾.
故②错误.
③△AGD与△OGD高相等.
若面积相等,则OG=AG=GF,
与OG<GF矛盾.故③错误
④由折叠可得,AE=EF,AG=GF,
同时可由∠AEG=∠AGE=67.5°,AE=AG,
得四边形AEFG是菱形.故④正确.
⑤由△BEF为等腰直角三角形,可得BE=![]() EF.
EF.
同理△GOF为等腰直角三角形,得GF=![]() OG.
OG.
所以BE=2OG.故⑤正确.
综上,①④⑤正确,故选D.
略








