已知：如图，在四边形ABCD中，AD=BC，AB=CD，E，F分别为AD，CB
延长线上一点，且DE=BF．
求证：∠E=∠F．

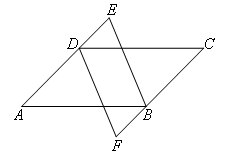
证明：如图，连接BD，

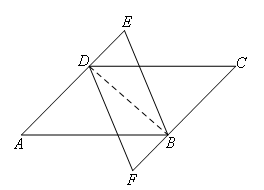
在△ADB和△CBD中

∴                    （SSS）
∴                        
∵∠ADB+∠EDB=180°
  ∠CBD+∠FBD=180°
∴∠EDB=∠FBD
在△EDB和△FBD中
                        
∴△EDB≌△FBD（     ）
∴∠E=∠F
请你仔细观察下列序号所代表的内容：
①△ADB≌△CBD；②△CBD≌△ABD；③∠ADB=∠CBD；④∠A=∠C；
⑤；⑥；⑦SSA；⑧SAS．
以上空缺处依次所填正确的是(    )

• A.②④⑤⑦
• B.①③⑥⑧
• C.②③⑥⑦
• D.①④⑥⑦

答案

正确答案：B

知识点：全等三角形的判定与性质  全等三角形证明过程训练  

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>