通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的，
下面是一个案例．
原题：如图1，点E，F分别在正方形ABCD的边BC，CD上，且∠EAF=45°，连接EF，易证EF=BE+DF．

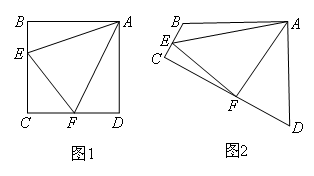
（1）类比联想
如图2，在四边形ABCD中，AB=AD，∠BAD=90°，点E，F分别在边BC，CD上，且∠EAF=45°．若∠B，∠D都不是直角，则当∠B与∠D满足等量关系         时，仍有EF=BE+DF．(    )

1．解题要点
①先研究图1，要证明EF=BE+DF，把△ADF绕点A逆时针旋转90°，此时AD与AB重合，点F落在点G处．通过旋转转移边角，证明△AEF≌△AEG，得到EF=EG，进而得到EF=BE+DF．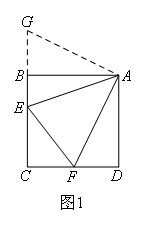

②照搬图1中的证明方法，利用旋转△ADF来转移边角关系，借助已知条件证明三角形全等，得到EF=BE+DF．
③在描述辅助线时，不能把旋转作为辅助线的作法（旋转不能由尺规作图实现），需要找到等价的方式来达到旋转的效果，
比如对于图1来说，辅助线应为“延长CB到点G，使BG=DF，连接AG”，
之后再去证明△ABG≌△ADF．
2．解题过程
当∠B+∠D=180°时，EF=BE+DF．
如图2，延长CB到点G，使BG=DF，连接AG．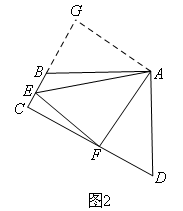

∵∠ABC+∠D=∠ABC+∠ABG=180°，
∴∠D=∠ABG．
∵AB=AD，BG＝DF，
∴△ABG≌△ADF（SAS），
∴AG=AF，∠BAG=∠DAF．
∵∠BAD=90°，∠EAF=45°，
∴∠BAE+∠DAF=45°，
∴∠BAE+∠BAG=∠EAG=45°，
∴∠EAG=∠EAF．
又∵AE=AE，
∴△AEF≌△AEG（SAS），
∴EG=EF．
∵EG=BE+BG，BG=DF，
∴EF=BE+DF．

略