如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,点E在AC边上,BE交CD于点G,EF⊥BE交AB于点F,且AC=mBC,CE=nEA(m,n为实数).试探究线段EF与EG之间的数量关系.
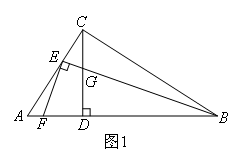
(1)如图2,当m=1,n=1时,EF与EG之间的数量关系为( )
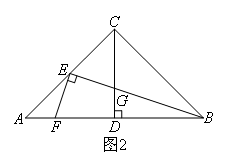
- A.
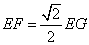
- B.
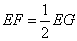
- C.EF=EG
- D.
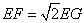
答案
正确答案:C
知识点:中考数学几何中的类比探究
如图2,过点E分别作EP⊥CD于点P,EQ⊥AB于点Q.
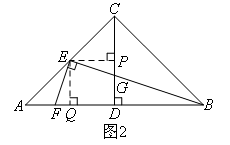
∵EP⊥CD,EQ⊥AB,CD⊥AB,
∴四边形EQDP是矩形,EP∥AD,
∴∠QEP=90°,∠CEP=∠EAQ.
∵∠BEF=90°,
∴∠FEQ=∠GEP.
又∵∠EQF=∠EPG,
∴△FEQ∽△GEP,
∴![]() .
.
∵∠A=∠A,∠EQA=∠BCA=90°,
∴△EQA∽△BCA,
∴![]() .
.
∵m=1,
∴![]() .
.
∵∠CEP=∠EAQ,∠EPC=∠AQE=90°,
∴△EPC∽△AQE,
∴![]() .
.
∵n=1,
∴![]() ,
,
∴![]() ,即EF=EG.
,即EF=EG.
略









