(上接第3题)(2)如图2,若BD,CE分别是△ABC的内角平分线,其他条件不变.
则FG和AB,BC,AC之间的关系为( )
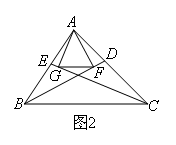
- A.
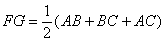
- B.
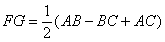
- C.
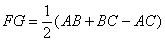
- D.
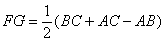
答案
正确答案:B
知识点:中考数学几何中的类比探究
1.解题要点
①图2和图1中,“BD,CE是角平分线”,“AG⊥CE,AF⊥BD”并没有发生变化,能用的三线合一没有发生变化,考虑照搬(1)中的思路,
首先作辅助线:延长AF交BC于点M,延长AG交BC于点N.
②同样可证△BFM≌△BFA,△CGA≌△CGN,同时![]() ,
,
结合MN=BM+CN-BC=AB+AC-BC,可得![]() .
.
③类比探究强调类比照搬,过程中照搬字母,照搬辅助线,做题时对应路线图来答题.
2.解题过程
如图,延长AF交BC于点M,延长AG交BC于点N.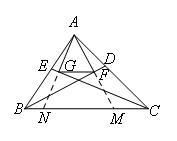
由题意得,∠ABF=∠MBF,∠BFA=∠BFM=∠AGC=∠NGC=90°,∠ACG=∠NCG.
∵BF=BF,CG=CG,
∴△BFM≌△BFA,△CGA≌△CGN,
∴AB=MB,AF=MF,AC=CN,AG=NG,
∴FG为△AMN的中位线,
∴![]() .
.
∵MN=MB+CN-BC=AB+AC-BC,
∴![]() .
.
略








