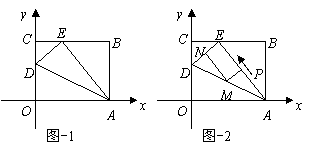
如图-1,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.
(1)在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标;
(2)如图-2,若AE上有一动点P(不与A,E重合)自A点沿AE方向向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(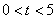 ),过P点作ED的平行线交AD于点M,过点M作AE的平行线交DE于点N.求四边形PMNE的面积S与时间t之间的函数关系式;当t取何值时,S有最大值?最大值是多少?
),过P点作ED的平行线交AD于点M,过点M作AE的平行线交DE于点N.求四边形PMNE的面积S与时间t之间的函数关系式;当t取何值时,S有最大值?最大值是多少?
(3)在(2)的条件下,当t为何值时,以A,M,E为顶点的三角形为等腰三角形,并求出相应的时刻点M的坐标
.
答案
(1)D点坐标为(0,![]() ),E点坐标为(2,4)
),E点坐标为(2,4)
(2)![]() ,当
,当![]() 时,
时,![]() 有最大值
有最大值![]() .
.
(3)![]() 或
或![]() 时,以A,M,E为顶点的三角形为等腰三角形,相应M点的坐标为
时,以A,M,E为顶点的三角形为等腰三角形,相应M点的坐标为![]() 或
或![]() .
.
知识点:运动变化型问题
(1)先研究基本图形.,
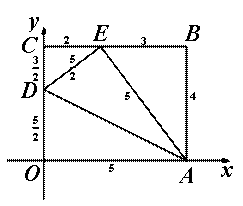
所以D点坐标为(0,![]() ),E点坐标为(2,4)
),E点坐标为(2,4)
(2)时间范围为0<t<5
AP=t,PE=5-t
如图①
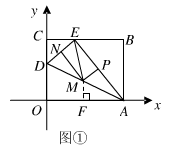
∵PM∥ED
∴△APM∽△AED,
![]() ,即
,即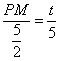 ,
,
∴PM=![]() ,AM=
,AM=![]()
而显然四边形PMNE为矩形,
![]()
又0<t<5
![]() 当
当![]() 时,
时,![]() 有最大值
有最大值![]() .
.
(3)分析知点A和点E为定点,M为动点
(i)若以AE为底,则ME=MA(如图①)
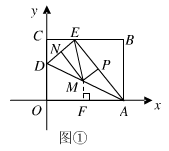
在△AEM中,ME=MA,且MP⊥AE于点P,
∴点P为AE中点,即AP=![]() AE=
AE=![]()
∵AP=t∴t=![]() (在0<t<5范围内,满足题意)
(在0<t<5范围内,满足题意)
此时M点坐标为![]() .
.
(ii)若以AE为等腰三角形的腰,则AM=AE=5(如图②)
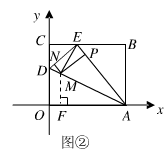
∵AM=![]()
∴![]() =5,则
=5,则![]() (在0<t<5范围内,满足题意)
(在0<t<5范围内,满足题意)
此时M点坐标为![]() .
.
综上,![]() 或
或![]() 时,以A,M,E为顶点的三角形为等腰三角形,相应M点的坐标为
时,以A,M,E为顶点的三角形为等腰三角形,相应M点的坐标为![]() 或
或![]() .
.
略








