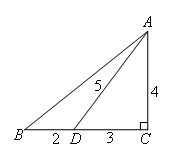
在△ABC中,∠C=90°,AC=4,BC=5,点D在BC上,并且CD=3,现有两个动点P,Q分别从点A和点B同时出发,其中点P以每秒1个单位长度的速度沿AC向终点C移动;点Q以每秒1.25个单位长度的速度沿BC向终点C移动.过点P作PE∥BC交AD于点E,连接EQ,设运动了x秒.
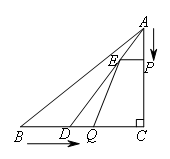
(1)设整个运动过程中,△EDQ的面积为y,则y与x的函数关系为( )
- A.
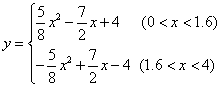
- B.
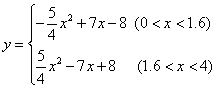
- C.
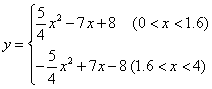
- D.
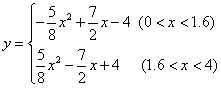
答案
正确答案:A
1.解题要点
①研究基本图形,将信息标注在图形上.
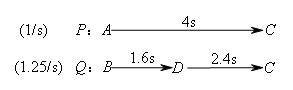
②分析运动状态,分段定范围.
∴![]() .
.
③分析几何特征、表达、设计方案求解.
要表达△EDQ的面积,直接利用公式.
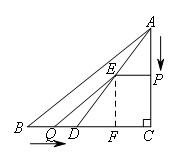
如图,过点E作EF⊥BC交BC于点F,所以![]() ,要表达QD,EF的长.
,要表达QD,EF的长.
由于点Q可能在点D的左侧或右侧,所以需要进行分类讨论,x的范围需要分段![]() (端点时,三角形不存在,所以端点值舍去).
(端点时,三角形不存在,所以端点值舍去).
2.解题过程
如图,过点E作EF⊥BC交BC于点F,

∴四边形EFCP是矩形,
∴EF=PC
由题意,![]()
∴BD=2,AD=5,PC=4-x,
①当![]() 时,点Q在线段BD上,
时,点Q在线段BD上,![]() ,
,
∴![]() .
.
②当![]() 时,点Q在线段DC上,
时,点Q在线段DC上,![]() ,
,
∴![]() .
.
∴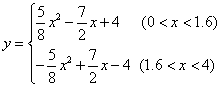
略








