如图，将矩形OABC放置在平面直角坐标系中，OA=8，OC=12，直线与x轴交于点D、与y轴交于点E，把矩形沿直线DE翻折，点O恰好落在AB边上的点F处，M是直线DE上的一个动点，直线DF上是否存在点N，使以点C，D，M，N为顶点的四边形是平行四边形？
小明的思路如下：①当定线段作为平行四边形的边时，通过    确定点的坐标；当定线段作为平行四边形的对角线时，则定线段绕中点    ，利用中点坐标公式确定点的坐标；②结合图形进行验证；③分析定点、动点。
小明的思路正确但排序混乱，请问正确的排序及划线部分应填入的关键词分别是(    )

• A.①③②；平移；旋转
• B.③①②；平移；旋转
• C.①③②；旋转；平移
• D.③①②；旋转；平移

答案

正确答案：B

知识点：平行四边形的存在性  

①首先可判断这是平行四边形存在性问题，那么先分析定点、动点．
定点：C，D，动点：M，N，理由如下：
∵直线与x轴交于点D、与y轴交于点E，
∴E（0，5），D（10，0），
∴OE=5.
由折叠，得EF=5.
∵OA=8，
∴AE=3，
∴AF=4，
∴点F（4，8），
∴直线DF：.
②两定点两动点的平行四边形存在性问题，连接两定点成为定线段，当定线段作为平行四边形的边时，通过平移确定点的坐标.如图，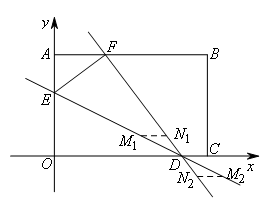

设，则
∴
解得
∴；
设，则
∴
解得
∴.
当定线段作为平行四边形的对角线时，则定线段绕中点旋转，利用中点坐标公式确定点的坐标.如图，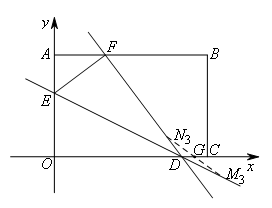

设，则
∴
解得
∴.
③结合图形验证.
综上，答案选B.

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>